
To convert a denary number for example 69, into binary write a 1 under the largest heading less than 69(i.e 64). You now have 69-64 = 5 remaining, to be converted into binary. 5 = 4+1
so put a 1 under 4 and 1 adn the rest are 0's.
To convert from denary to binary first make a table as show below with headings of 1,2,4,8,...128 from right to
left.(if the number is greater than 255 continue writing the headings).

To convert a denary number for example 69, into
binary write a 1 under the largest heading less than 69(i.e 64). You now have 69-64 = 5 remaining, to be converted
into binary. 5 = 4+1
so put a 1 under 4 and 1 adn the rest are 0's.

Binary addition works in a similar way to denary addition. If the two number being added together are equal to or
greater than the base value,(in the case of denary, 10) then the 'tens' value is carried over. In binary if the
addition results into 2 or more it has to be carried over to the next column.
Rules for addition in binary:
1. 0+0 = 0
2. 0+1 = 1
3. 1+0 = 1
4. 1+1 = 0 Carry 1(this is 2 in denary or 10 in binary)
5. 1+1+1 = 1 Carry 1(this is 3 in denary or 11 in binary)
Take for example 2 numbers 12 and 14. To add them in binary first they will have to be converted to binary
12 -> 1100
14 -> 1110
This is what it would look like to add the 2 numbers in binary
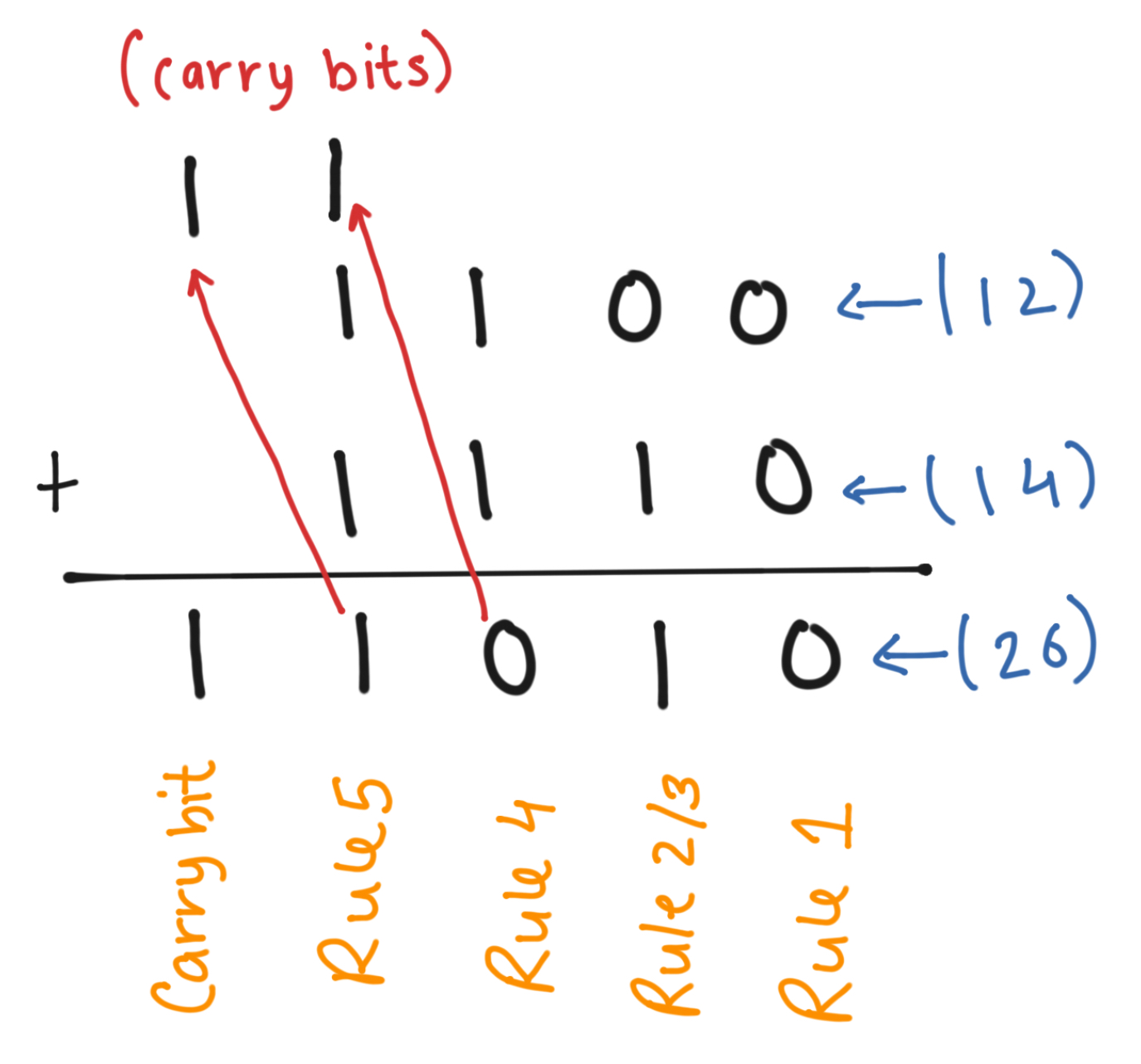
This is what it would look like to add the 2 numbers in binary
(Enter Number 1 and 2 in binary)
Num 1:(Enter Number 1 and 2 in binary)
Num 1:(Enter Number 1 and 2 in binary)
Num 1:(Enter Number 1 and 2 in binary)
Num 1: