My Homework for Chapters 47-49, textbook pages 259-268
Computational thinking
Definition of computational thinking: Thinking about how a problem can be solved. (has 2 main steps)
- Formulate the problem as a computational problem (solvable by using an algorithm)
- Construct an algorithm to solve it
However, it is not just about solving the problem using an algorithm, but most importantly doing so efficiently!
Abstraction
Definition of Abstraction: Ignoring the unnecessary details of a problem, and focusing on important aspects of it.
Fundamentally, Abstraction frees programmers from the distractions of irrelevant technological details when designing algorithms.
Origins of graph Theory
Around 200 years ago, a problem arose in the old Prussian city of Königsberg.
The locals liked to stroll around the city and cross each bridge once and once only, or alternatively prove that it was impossible.
Eventually the Mayor turned to the the mathematician - Euler to solve this problem.
Euler began by removing the irrelevant details from the map and simplify it into the only components of the problem that he needed.
From this:
 Original Map of Königsberg's bridges
Original Map of Königsberg's bridges
 Euler's first simplified drawing
Euler's first simplified drawing
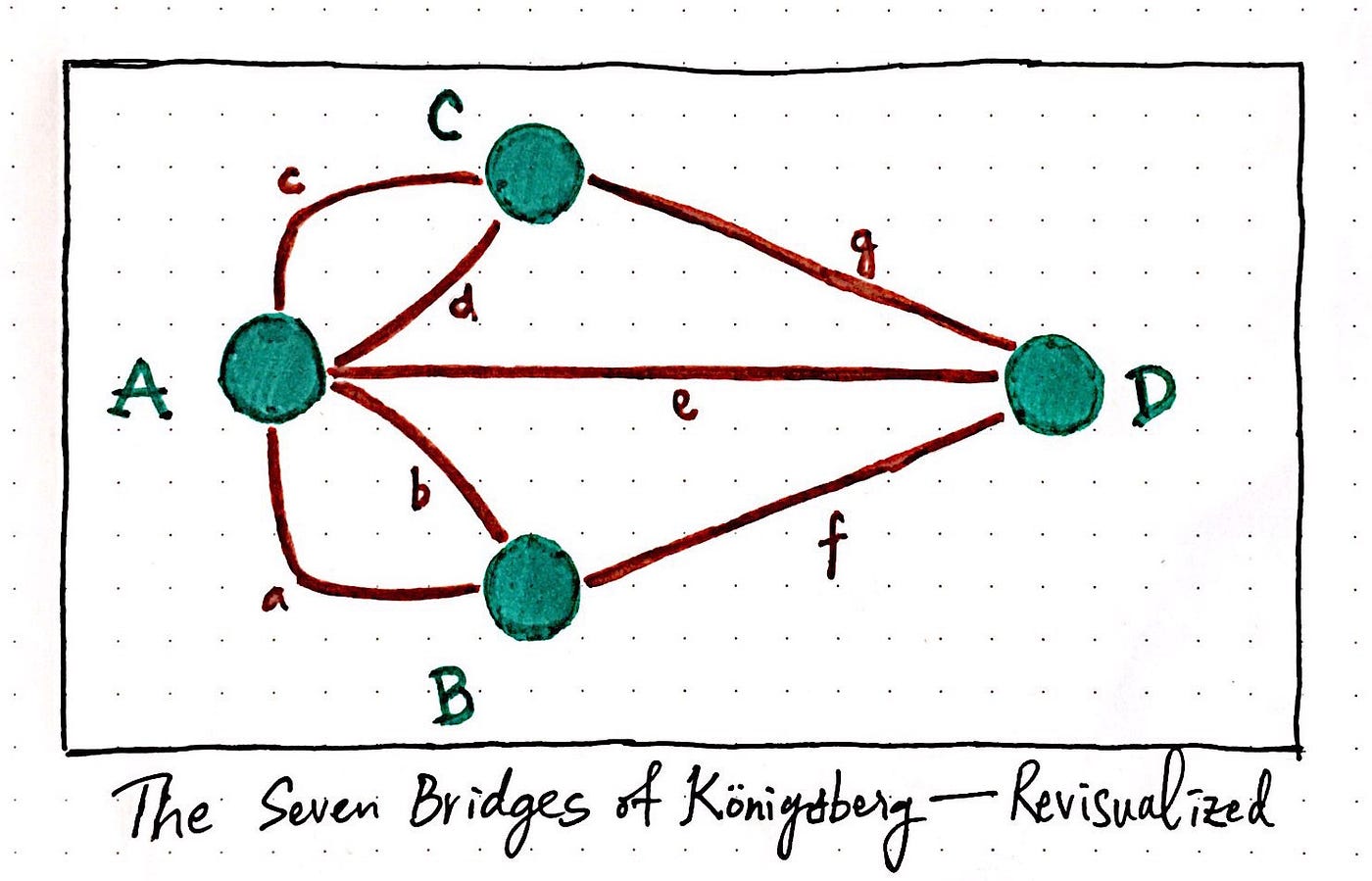 To constructing the very first graph!
To constructing the very first graph!
That day Euler did something revolutionary, constructing the first graph, and creating the "Euler Path".
To read more about how he actually solved the problem click here.
Representational abstraction is a representation arrived at by removing unnecessary details.
Data Abstraction
Definition of Abstract Data Types: A theoretical model for a data structure that specifies a set of operations and properties without specifying the implementation details.
Examples of abstract data types:
As programmers, we use their in-built functions and capabilities but do not need to worry about their implementation. (i.e: dequeue, enqueue, pop, peek)
Pre-conditions:
Giving functions certain parameters will cause them to crash, making it important to add constraints on the inputs of a program.
For example, a program looking for the square root may be unable to have negative inputs (as it doesn't work in the context/implementation of the function).
Due to this fact, it is vital that we specify the pre-conditions of a program within its documentation. (i.e: The input must be non-negative for a square root function).
Advantages of pre-conditions:
Specifying pre-conditions as part of the documentation of a subroutine ensures that the user knows the constraints of the subroutine and what checks must be carried out on inputs before passing it to the subroutine - so that it works.
Caching:
Caching is a process done automatically by the OS, however its benefits can still be used by programmers.
Simply put caching is the temporary storage of program instructions or data that have been used once and may be used again shortly.
This feature is particularly useful in many recursive functions (such as finding the nth fibonacci number).
 Here is the runtime difference between a function that uses caching versus one that does not, the difference is clear.
Click here to see code
Here is the runtime difference between a function that uses caching versus one that does not, the difference is clear.
Click here to see code
Although the optimisation may not be as noticable as this one, in many cases caching is an extremely useful tool in optimising programs.



