I spent too much time researching and writing the project and didn't give myself enough time to make diagrams and a a result the last half of the website is just a text dump. This deffinatly isn't on the spec but I was researching algorithms and I found this too interesting to not do the homework on. Another possible issue is the technology is very new so it's fully possible that things have changed since the rescorces I used and the information is outdated but this isn't the case as far as I am aware. I would add more diagrams but I've spent three hours on it and I unfortunatly have other homework.
Ciphers are a way of making text/messages illegable so that only people with a decyphering code can understand. A basic example of this is the Ceaser cypher :
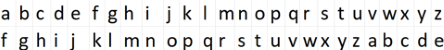
A ceaser cipher is where all of the letters in the alphabet are shifted the same amount along the alphabet. For example a = f, b = g, etc. As you can imagine this is very easy to break with a basic iteration loop.
For acctually protecting data in messages we need much more secure systems for hiding information and this is esspecially important for the internet.
One of the main issues with the Ceaser cypher and others like it is that is it symmetric, meaning the same code (fomrally known as key) to encrypt and decrypt the message. This is very problematic for the internet as for that to work the key would need to be transmitted accross the internet making it succeptable to interception meaning it isn't really secure. The solution to this issue is asymmetric encryption
Asymmetric encryption utilises two keys, a public key and a private key. The public key encrypts data while the private key decrypts it. The private key can't be reverse engineered from a decrypted message or the public key (hence the name) meaning the public key can be sent accross the internet without fear. The way this is typically done is by having the public key be a very large multiple of 2 prime numbers and the encryption key being those two prime numbers. Because there isn't an easy formulla for finding prime factors of a number (other than just lots of guess work) and there isn't a formula for finding prime numbers, it takes current computers years to break through the private keys.
I previously said there was no way of working out the prime factors of a number but that isn't entirely true. Factors of numbers can be deduced from Shor's algorithm:
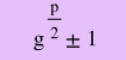
The basis of Shor's algorithm is that if you have two numbers: x and y, x to the power of p (where p is an integer) = ay +1 (where a is an integer). Basically:
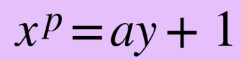
To give an example if we pick two numbers: 42 and 13. 42 squared = 1764 = 13 X 135 + 9 which doesn't work but 42 cubed = 74088 = 13 X 5699 + 1. So Shor's algorithm will produce a multiple of y.
Regular computers struggle with this because you still have to guess what p is so it still just ends up being guessing.
The equation can be rearanged by taking away one from both sides and using the difference of two squares law to produce:
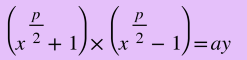
Now we have the equation in a form such that one number X another number = ay meaning they're two facotrs. This can produce factors of ay rather than of y but using Euclid's algorithm you can find common factors between the two factors of ay and multiply them to get a factor of y
Some issues such as one of the two results being a factor of y making the other number a factor of a or if p is odd it likely won't be an integer but these are easily fixable issues. The main issue is still guessing p. This problem is fixed with quantum superposition: Normal computers will test a number to check if it works then check another and another etc. taking a very long time but quantum computers can enter multiple guesses at once and will then spit out a random (weighted) one of the results as shown in the diagram below:

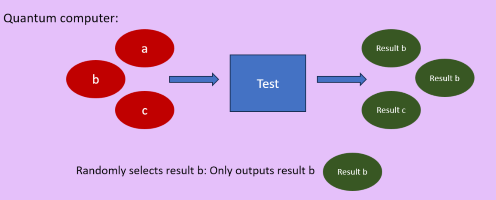
You have to get through the random selection by making all the unsuccessful results cancel each other out. We do this by having the input be x to the power of u (where u is an integer and u = p/2) and the out being x and the difference between the result of x to the power of u and the closest factor of y lower than x to the u. p has a repeating property meaning the difference between the closest lower power of y: for x to the power of u = x to the power of u + p. estentialy the remainder is the same for x to the u and x to the u+p and x to the u+2p etc. This means if you make the output of the quantum computer to just be a remainder then it will only leave specific powers such that the remainder is always than output. For example if the output is a remainder of three then you'll be left with all the values of u such than x to the u is 3 higher the the closest lower multiple of y. From these remaining values of u the difference between each u value will be p (due to the repeating property). Esentially the 1st output of the quantum computer will just be a remainder. This means we are only left with values of u such that x to the u has the same remainder. The difference between each value of u for the consecutive powers that result in that specific remainder will be p.
Finally you but the sequence of the values of u into a Fourier transform which will output a sine wave with a frequency of 1 divided by p. This works using a quantum Fourier trnasform: if you put one into a quantum Fourier transform it will output a sequence of all numbers but each number is weighted such that they combine in the shape of a sine wave, if 2 is the input then the output will be a sine wave just like the output for 1 but with a higher frequency. If you input a sequence of numbers then the output will be a sequence of sequences which is effectivly a sequence of sine waves each with a different frequency depending on the values. These sine waves add together, subtract from one another or cancel out. If you input a sequence of values each with a set differnce then the output will cancel out to be just be a state representing 1 divided by the difference the difference. Meaning if you input the sequence of values of u that all have the same remainder then the output will cancel out to a representation of the value of 1 divided by p. You then find the reciprocal and if it's even then you have the value for p. Finally you raise any integer (greater than 1) to the power of p over 2 plus or minus 1 and if one of those values isn't a multiple of y then those values share common factors which are the prime factors that multiply together to make the public key. Meaning you have the private key and can steal all the data, good for you. Luckily this takes lots of storage that modern quantum computers don't have so we're safe (for now).